網路上有各式各樣的地圖出現,背後的運算就有很多的演算法、資料庫和參數來支持。還記得之前討論過有關圖的深度及廣度搜尋,就有提到過怎麼找最短的路徑,而這只是其中最基礎的幾個概念而已。現今的程式運算其實都更複雜,效率也更高,都是以前科學家的發明,還有工程師的發展,我們才有這些科技可用。
回到今天的主題,來介紹一個號稱核心概念只有五行的演算法:Floyd-Warshall 演算法。
先來看我們今天要走的圖: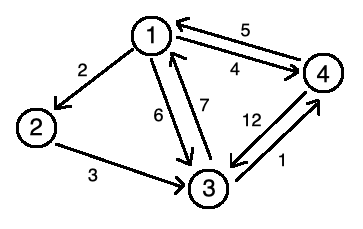
我們現在要找的是任意兩個點之間的最短路徑,也稱作「多源最短路徑」。
首先,一樣先將圖的資訊存到二為矩陣中。
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 2 | 6 | 4 |
| 2 | ∞ | 0 | 3 | ∞ |
| 3 | 7 | ∞ | 0 | 1 |
| 4 | 5 | ∞ | 12 | 0 |
| 如果我們要求任意兩個點的最短距離,但有些點不能直達,勢必要有經過中間點才行。 | ||||
| 我們來看看以下的分析: |
4 → 3 為 12
4 → 1 → 3 為 11
4 → 1 → 2 → 3 為 10
我們只要透過多次的中轉,和初始的路徑比較,如果能讓兩點之間的路徑變短,就更新。好比 4 到 3 的原始距離為 12,4 到 1 的距離為 5,加上 1 到 3 的距離為 6 共 11,比原始 12 小,我們就讓二為矩陣中 4 到 3 的距離更新為 11 。因為我們只看最短路徑,不討論最少的中轉次數,所以可以這麼做。
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 2 | 6 | 4 |
| 2 | ∞ | 0 | 3 | ∞ |
| 3 | 7 | ∞ | 0 | 1 |
| 4 | 5 | ∞ | 11 | 0 |
| 同理,我們把 4 到 1 的距離為 5,加上 1 到 2 的距離為 2,加上 2 到 3 的距離為 3 共 10,比原始 11 小,再更新回矩陣中。 | ||||
| 1 | 2 | 3 | 4 | |
| - | - | - | - | - |
| 1 | 0 | 2 | 6 | 4 |
| 2 | ∞ | 0 | 3 | ∞ |
| 3 | 7 | ∞ | 0 | 1 |
| 4 | 5 | ∞ | 10 | 0 |
| 根據以上的概念,發現每一個點都有可能使另外兩個點之間的路徑變的更短。所以程式碼的主要概念就是用迴圈來跑,並進行比較,再更新。 |
import numpy as np
import pandas as pd
inf = 99999999
e = np.zeros((10,10), dtype = np.int)
n, m = map(int, input().split(' '))
#initialize
for i in range(1, n+1):
for j in range(1, n+1):
if i==j:
e[i][j]=0
else:
e[i][j]=inf
#read line
for i in range(1, m+1):
t1, t2, t3 = map(int, input().split(' '))
e[t1][t2]=t3
#Floyd-Warshall algorithm
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
if e[i][j] > e[i][k]+e[k][j]:
e[i][j] = e[i][k]+e[k][j]
# test data:
# 4 8
# 1 2 2
# 1 3 6
# 1 4 4
# 2 3 3
# 3 1 7
# 3 4 1
# 4 1 5
# 4 3 12
#output final consequences
for i in range(1, n+1):
print(e[i][1:n+1])
# ---------------------
# [0 2 5 4]
# [9 0 3 4]
# [6 8 0 1]
# [ 5 7 10 0]
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 2 | 5 | 4 |
| 2 | 9 | 0 | 3 | 4 |
| 3 | 6 | 8 | 0 | 1 |
| 4 | 5 | 7 | 10 | 0 |
但 Floyd-Warshall 演算法不能解決帶有「負權迴路」的圖,因為帶有負權迴路的圖並沒有最短路徑。有興趣可以自己拿筆畫畫看就會知道了。
